
[PAPER 2]
Essay
[60 marks]
Answer eight questions in all: five questions from Part I and three questions from Part II.
PART I
[15 marks]
Answer any five questions from this part.
All questions carry equal marks.
1. (a) What is a dimensionless quantity?
(b) The frictional force, f, between a box of mass m and a table is given by:
$$f = \mu mg$$
where \( g \) is the acceleration due to gravity. Show that the coefficient of friction, \( \mu \), is dimensionless.
[3 marks]
Answers to Question 1a - b
1. (a) A dimensionless quantity is a physical quantity that has no units and is expressed as a pure number. It is typically the ratio of two quantities with the same dimensions, such as angles (in radians), refractive index, or the coefficient of friction.
(b) From the formula:
$$f = \mu mg$$
Solving for \( \mu \):
$$\mu = \frac{f}{mg}$$
Now, analyzing the dimensions:
So, \( mg \) has dimensions:
$$[M][LT^{-2}] = [MLT^{-2}]$$
Therefore:
$$\mu = \frac{[MLT^{-2}]}{[MLT^{-2}]} = 1$$
Hence, \( \mu \) is a dimensionless quantity.
2. (a) Define spring constant, \( k \), of a spring.
(b) A helical spring is stretched by an amount \( e \), under a constant force \( F \). Show that the energy stored in the spring depends only on \( k \) and \( e \).
[3 marks]
Answers to Question 2a - b
2. (a) The spring constant \( k \) is a measure of the stiffness of a spring. It is defined as the force required to produce a unit extension or compression in the spring.
Mathematically:
$$F = ke$$
where \( F \) is the force applied and \( e \) is the extension of the spring.
(b) The energy \( E \) stored in a stretched spring is given by the formula:
$$E = \frac{1}{2}Fe$$
But from Hooke’s Law, \( F = ke \), so substituting into the energy formula:
$$E = \frac{1}{2}ke \cdot e = \frac{1}{2}ke^2$$
Hence, the energy stored in the spring depends only on \( k \) and \( e \).
3. (a) What is a laser?
(b) State two uses of a laser beam.
[3 marks]
Answers to Question 3a - b
3. (a) A laser (Light Amplification by Stimulated Emission of Radiation) is a device that emits a narrow, highly focused beam of coherent light through the process of stimulated emission.
(b) Two uses of a laser beam:
1. In medicine, for eye surgery and removing tumors.
2. In technology, for reading data in CDs/DVDs and barcode scanners.
4. State one application of a magnet in each of the following areas of activity:
(a) Exploration and Navigation;
(b) Industry and Constructional sites;
(c) Medical.
[3 marks]
Answers to Question 4a - c
(a) Exploration and Navigation: Magnets are used in compasses to determine direction by aligning with the Earth's magnetic field.
(b) Industry and Constructional sites: Magnets are used in cranes to lift and move heavy metal objects like scrap iron.
(c) Medical: Magnets are used in MRI (Magnetic Resonance Imaging) machines to produce detailed images of organs and tissues.
5. Draw a section of the structure of a fibre optics cable showing:
(a) the core;
(b) the cladding;
(c) signal transmission through it.
[3 marks]
Answer to Question 5a - c
Diagram: Structure of a Fibre Optics Cable
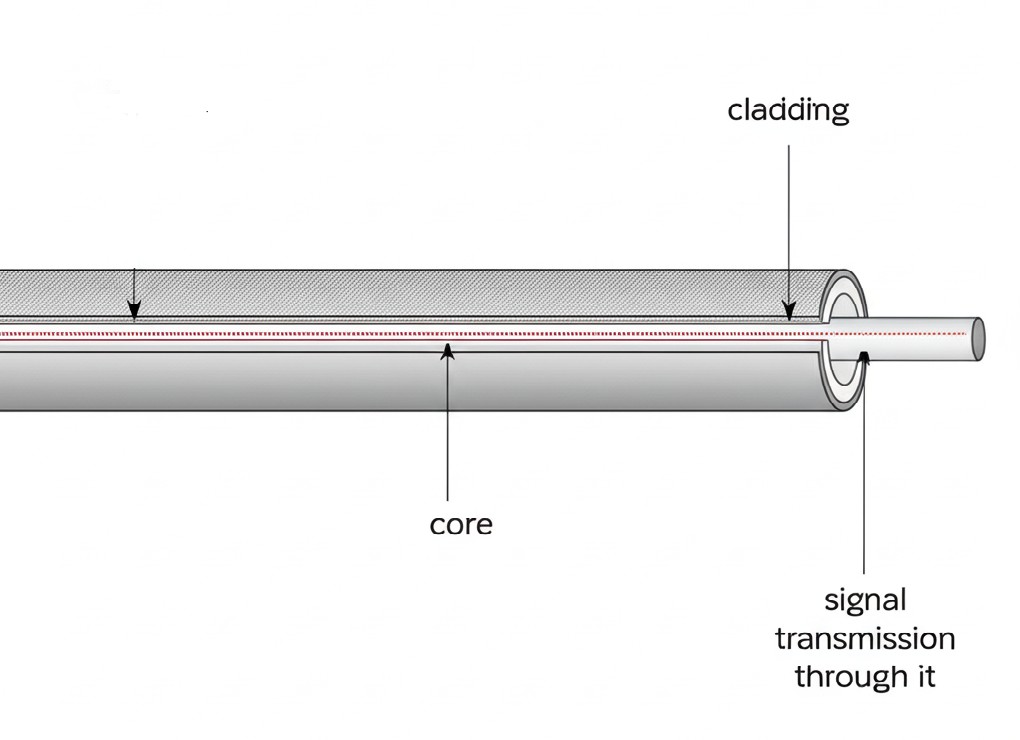
Labelled features:
6. (a) What is a parking orbit?
(b) State the uses of a geostationary satellite.
[3 marks]
Answers to Question 6a - b
6. (a) A parking orbit is an intermediate orbit where a spacecraft stays temporarily before moving to its final orbit or destination.
(b) Uses of a geostationary satellite:
1. For television broadcasting and communication services.
2. For weather monitoring and forecasting.
3. For navigation systems such as GPS augmentation.
7. A missile aimed at a target on a wall 12.5 m high is fired at \(24.0 \, \text{m/s}\). Determine and state whether or not the target will be hit when the angle of projection is \(40^\circ\).
\([g = 10 \, \text{m/s}^2]\)
[3 marks]
Answer to Question 7
Given:
Solution:
Vertical component of velocity:
\(u_y = u \sin \theta\)
\(= 24.0 \times \sin 40^\circ\)
\(= 15.43 \, \text{m/s}\)
Time to reach height \(h\) (using \(s = u_yt - \frac{1}{2}gt^2\)):
\(12.5 = 15.43 t - 5 t^2\)
Rearranged: \(5 t^2 - 15.43 t + 12.5 = 0\)
Solving quadratic equation:
\(t = \frac{15.43 \pm \sqrt{(15.43)^2 - 4 \times 5 \times 12.5}}{2 \times 5}\)
\(t = \frac{15.43 \pm \sqrt{238.11 - 250}}{10}\)
Since discriminant is negative (\(238.11 - 250 = -11.89\)), no real solution for \(t\), meaning the missile does not reach the height of 12.5 m.
Conclusion: The missile will not hit the target on the wall at 12.5 m height when fired at \(40^\circ\) with the given velocity.
PART II
[45 marks]
Answer three questions from this part.
All questions carry equal marks
8. (a) Explain the term moment of forces.
[3 marks]
(b) A uniform metal tube of length 10 m and mass 100 kg is suspended horizontally by two flexible cords attached at 100 cm and 300 cm respectively from the ends of the tube. Find the tension in each of the cords. [g = 10 m/s2]
[4 marks]
(c) (i) With the aid of a diagram explain two types of equilibrium.
(ii) State two examples of couple.
[4 marks]
(d) A uniform cylindrical object with height 0.8 m and base diameter 0.4 m is placed on an inclined plane. If the plane makes an angle \(\theta\) with the horizontal such that it is just enough to make the object topple, calculate the value of \(\theta\).
[4 marks]
Answers to Question 8 (a) - (d)
8. (a) Moment of force is the turning effect of a force about a pivot or point. It is given by the product of the force and the perpendicular distance from the pivot to the line of action of the force.
(b) Given:
Total weight:
\[ W = mg = 100 \times 10 = 1000\, \text{N} \]
Cord attachment points from the left end: \(d_1 = 1\, \text{m}\), \(d_2 = 3\, \text{m}\)
Let \(T_1\) and \(T_2\) be the tensions in the cords.
Taking moments about the left end:
\[ T_1 \times 1 + T_2 \times 3 = 1000 \times 5 \]
\[ T_1 + 3T_2 = 5000 \]
From vertical equilibrium:
\[ T_1 + T_2 = 1000 \]
Substitute \(T_2 = 1000 - T_1\) into the moment equation:
\[ T_1 + 3(1000 - T_1) = 5000 \]
\[ T_1 + 3000 - 3T_1 = 5000 \]
\[ -2T_1 = 2000 \]
\[ \Rightarrow T_1 = -1000\, \text{N} \]
Since tension can't be negative: \(T_1 = 0\), \(T_2 = 1000\, \text{N}\)
(c)(i) Types of equilibrium:
(ii) Examples of a couple:
(d) Given:
Radius, \(r = \frac{d}{2} = 0.2\, \text{m}\)
Condition for toppling: line of action of weight reaches edge of base
\[ \tan \theta = \frac{r}{h} = \frac{0.2}{0.8} \]
\[ \tan \theta = 0.25 \]
\[ \Rightarrow \theta = \tan^{-1}(0.25) \]
\[ \theta \approx 14^\circ \]
9. (a) Explain the statement the linear expansivity of a body is \(3.0 \times 10^{-9}\, \text{K}^{-1}\).
[2 marks]
(b) Explain why power lines are always connected in sag.
[3 marks]
(c) An iron tyre of diameter 60 cm, at 20 °C is to be shrunk onto a wheel of diameter 60.45 cm. If the tyre is to be heated to a temperature \(T\) so as to slip over the wheel, calculate \(T\). [Linear expansivity of iron = \(1.2 \times 10^{-5}\, \text{K}^{-1}\)]
[2 marks]
(d) State two merits each of:
(i) Thermoelectric thermometer;
(ii) Constant volume gas thermometer.
[4 marks]
(e) State four effects of heat on a substance.
[4 marks]
Answers to Question 9 (a) – (e)
9. (a) It means that for every rise in temperature of 1 K, the length of the body increases by \(3.0 \times 10^{-9}\) times its original length.
(b) Power lines are connected in sag to allow for expansion during hot weather and contraction during cold weather. Without sag, the lines may break when they contract in cold weather due to tensile stress.
(c) Given:
\[ \Delta D = \alpha D_1 (T - T_1) \]
\[ 60.45 - 60 = 0.45 \]
\[ 1.2 \times 10^{-5} \times 60 = 7.2 \times 10^{-4} \]
\[ 0.45 = 7.2 \times 10^{-4} (T - 20) \]
\[ 0.45 = 7.2 \times 10^{-4} (T - 20) \]
\[ T - 20 = \frac{0.45}{7.2 \times 10^{-4}} \approx 625 \]
\[ T = 625 + 20 = 645^\circ\text{C} \]
(d)
(i) Merits of Thermoelectric thermometer:
(ii) Merits of Constant volume gas thermometer:
(e) Effects of heat on a substance:
10. (a) (i) Distinguish between pole and center of curvature of a spherical mirror.
(ii) Describe how the approximate focal length of a concave mirror could be determined.
[4 marks]
(b) A concave mirror of focal length 10 cm forms a magnified image on a screen 15 cm from the object. Calculate the image distance.
[4 marks]
(c) A spot at the bottom of a vessel of uniform cross-sectional area 10 cm2 filled with alcohol of volume 75 cm3 appeared to be displaced by 2 cm when viewed vertically at the top. Calculate the refractive index of the alcohol.
[4 marks]
(d) Explain why the pitch of the sound produced by a guitar increases when its string is tightened.
[3 marks]
Answers to Question 10 (a) - (d)
10. (a) (i)
Pole: The pole is the midpoint or the vertex of the spherical mirror, where the principal axis meets the mirror.
Center of curvature: The center of curvature is the center of the sphere from which the mirror segment is taken; it lies on the principal axis at a distance equal to the radius of curvature from the pole.
(ii) The approximate focal length of a concave mirror can be determined by focusing a distant object (like the sun) on a screen and measuring the distance between the mirror and the screen, which approximates the focal length.
(b) Given:
Using the mirror formula:
\[ \frac{1}{f} = \frac{1}{v} + \frac{1}{u} \]
\[ \frac{1}{10} = \frac{1}{v} + \frac{1}{-15} \]
\[ \frac{1}{v} = \frac{1}{10} - \frac{1}{15} \]
\[ = \frac{3}{30} - \frac{2}{30} = \frac{1}{30} \]
\[ v = 30\, \text{cm} \]
(c) Given:
Calculate actual depth \(h\):
\[ h = \frac{V}{A} = \frac{75}{10} = 7.5\, \text{cm} \]
Refractive index \(n\):
\[ n = \frac{\text{Real depth}}{\text{Apparent depth}} \] \[ = \frac{7.5}{7.5 - 2} \]
\[ = \frac{7.5}{5.5} \approx 1.36 \]
(d) Tightening the guitar string increases the tension, which increases the frequency of vibration, thereby raising the pitch of the sound produced.
11. (a) State two factors that determine the sensitivity of a moving-coil galvanometer.
[2 marks]
(b) (i) A bulb is connected to a source of electricity. State two effects of adding more bulbs in series with the first one.
(ii) An electrical technician wishes to reduce the current passing through a galvanometer to 0.05 times its initial value by means of a resistor. The internal resistance of the galvanometer is 100 Ω.
[5 marks]
(c) Explain why a voltmeter is always connected across a load.
[2 marks]
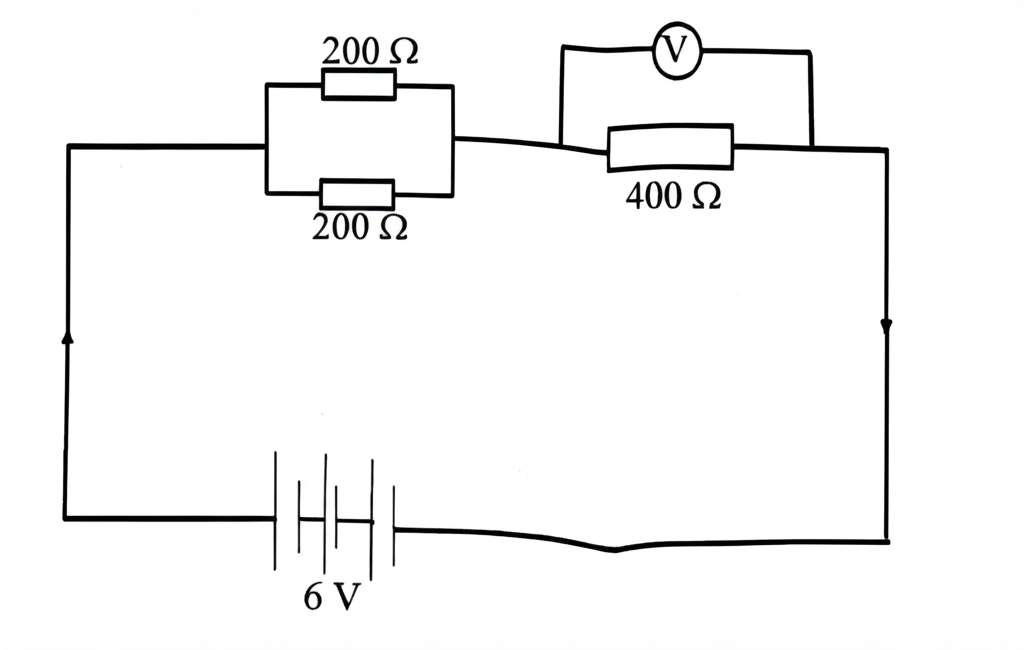
(d) The figure below is a circuit diagram. Calculate the reading on the voltmeter across the 400 Ω resistor.
[6 marks]
Answers to Question 11 (a - d)
11. (a) Two factors that determine the sensitivity of a moving-coil galvanometer are:
– The number of turns in the coil (more turns increase sensitivity)
– The strength of the magnetic field (stronger field increases sensitivity)
(b) (i) Two effects of adding more bulbs in series with the first one:
– The total resistance of the circuit increases, reducing the current.
– The brightness of each bulb decreases due to reduced current.
(b) (ii α)
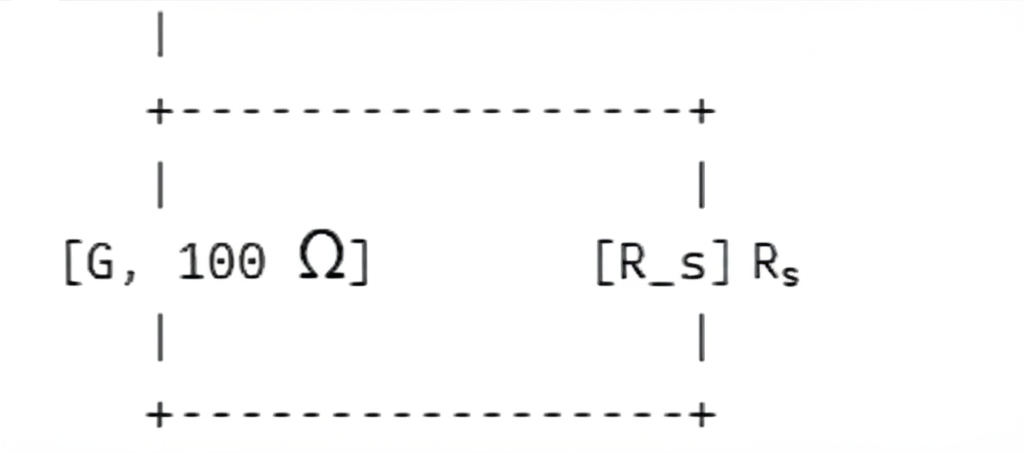
(b) (ii β) To reduce the current in the galvanometer to 0.05 of its original value:
Let \( R_s \) be the resistance of the shunt resistor, and \( R_g = 100\,\Omega \) the internal resistance of the galvanometer.
Using current division:
$$\frac{I_g}{I_s} = \frac{R_s}{R_g}$$
$$\frac{0.05I}{0.95I} = \frac{R_s}{100}$$
$$\Rightarrow R_s = \frac{100}{19} \approx 5.26\,\Omega$$
(c) A voltmeter is always connected across a load to measure the potential difference (voltage) between two points. It must be in parallel to avoid significantly affecting the circuit current.
(d) In the given circuit:
– Two 200 Ω resistors are in parallel: \( R_{eq} = 100\,\Omega \)
– Total resistance: \( R_{total} = 100 + 400 = 500\,\Omega \)
– Current: \( I = \frac{6\,V}{500\,\Omega} = 0.012\,A \)
– Voltage across 400 Ω resistor:
\( V = IR = 0.012 \times 400 \)
\( = 4.8\,V \)
Therefore, the voltmeter reads: 4.8 V
12. (a) (i) Define count rate as applied to radiation detection.
(ii) State how the count rate is related to the activity of a sample.
[3 marks]
(b) When is radioactive process said to be:
(i) spontaneous?
(ii) random?
[4 marks]
(c) State three applications of radioisotope in medicine.
[3 marks]
(d) A radioactive sample decreases by \(\Delta N\) in an interval of \(\Delta t\) such that the number of undecayed nuclei in it is \(N\). Using the information provided, write an expression for the:
(i) activity of the sample;
(ii) decay constant.
[2 marks]
(e) An electromagnetic radiation of frequency \(1.3 \times 10^{15} \, \text{Hz}\) is incident on an aluminum surface and the maximum speed of photoelectrons emitted from the surface is \(5.6 \times 10^{5} \, \text{m/s}\). Calculate the work function of Aluminum.
[mass of electron = \(9.1 \times 10^{-31} \, \text{kg}\)] [Planck's Constant = \(6.6 \times 10^{-34} \, \text{Js}\)]
[3 marks]
Answers to Question 12 (a) - (e)
12. (a) (i) Count rate is the number of radiation counts detected per unit time.
(ii) The count rate is directly proportional to the activity of the radioactive sample.
(b) (i) Radioactive process is spontaneous if it occurs without any external cause or influence.
(ii) Radioactive process is random if it is impossible to predict when a particular nucleus will decay.
(c) Applications of radioisotopes in medicine:
12. (d) (i) Activity, \(A\):
\[ A = -\frac{\Delta N}{\Delta t} \]
(ii) Decay constant, \(\lambda\):
\[ \lambda = \frac{A}{N} \]
\[ \lambda = -\frac{1}{N} \times \frac{\Delta N}{\Delta t} \]
12. (e) Given:
\[ f = 1.3 \times 10^{15} \text{ Hz} \]
\[ v = 5.6 \times 10^{5} \text{ m/s} \]
\[ m = 9.1 \times 10^{-31} \text{ kg} \]
\[ h = 6.6 \times 10^{-34} \text{ Js} \]
Photon energy, \(E\):
\[ E = h \times f \]
\[ = (6.6 \times 10^{-34}) \times (1.3 \times 10^{15}) \]
\[ = 8.58 \times 10^{-19} \text{ J} \]
Kinetic energy of electron, \(KE\):
\[ KE = \frac{1}{2} m v^2 \]
\[ = \frac{1}{2} \times 9.1 \times 10^{-31} \]
\[ \times (5.6 \times 10^{5})^2 \]
\[ = 1.43 \times 10^{-19} \text{ J} \]
Work function, \(\phi\):
\[ \phi = E - KE \]
\[ = 8.58 \times 10^{-19} - 1.43 \times 10^{-19} \]
\[ = 7.15 \times 10^{-19} \text{ J} \]