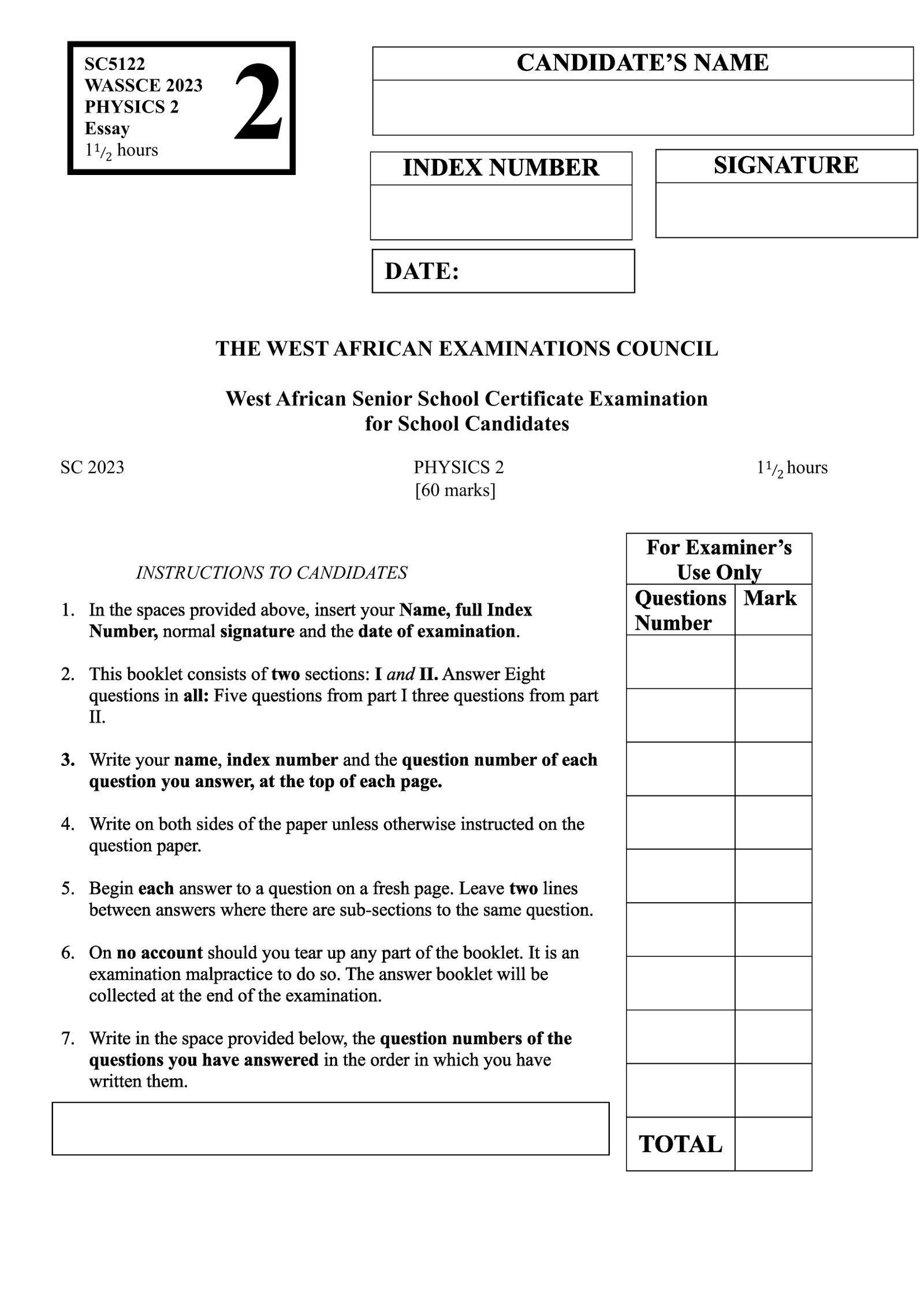
1. A thin aluminium wire is gradually stretched until it breaks. Sketch a force-extension graph for the wire and on the graph indicate the:

(a) Elastic limit;

(b) Maximum load.

[4 marks]

Answers to Question 1a - b

2. (a) State one disadvantage of fibre optic cables as compared to copper cables in the telecommunication industry.

(b) Name two applications of fibre optics in the medical field.

[3 marks]

Answers to Question 2a - b

2. (a) One disadvantage of fibre optic cables is that they are more expensive and fragile compared to copper cables, making installation and maintenance more complex.

(b) Two applications of fibre optics in the medical field:

1. In endoscopy, to view internal organs with minimal invasion.

2. In laser surgeries, to deliver precise laser light for procedures like tumor removal or corrective eye surgery.

3. (a) What are ferromagnetic materials?

(b) Name two elements in the periodic table that are ferromagnetic.

[3 marks]

Answers to Question 3a - b

3. (a) Ferromagnetic materials are substances that can be strongly magnetized in the presence of a magnetic field and retain their magnetism even after the external field is removed.

(b) Two ferromagnetic elements:

1. Iron (Fe)

2. Nickel (Ni)

4. The mutual force, F, between two bodies, their distance apart, r, and the product of their masses, m, are related to the universal gravitational constant, G, by the formula:

$$F = \frac{Gm}{r^2}$$

Show that the formula is dimensionally correct.

[3 marks]

Answer to Question 4

Given: $$F = \frac{Gm}{r^2}$$

Step 1: Find the dimensions of each quantity.

• Force, F has dimension: \( [F] = MLT^{-2} \)
• Mass product, m (assumed as \( m_1 \cdot m_2 \)): \( [m] = M^2 \)
• Distance, r: \( [r] = L \)

Step 2: Rearranging the formula to find the dimension of \( G \):

$$G = \frac{Fr^2}{m}$$

Step 3: Substituting the dimensions:

$$[G] = \frac{MLT^{-2} \cdot L^2}{M^2}$$

$$= \frac{ML^3T^{-2}}{M^2}$$

$$= M^{-1}L^3T^{-2}$$

Step 4: Now verify the right-hand side of the original equation:

$$\frac{Gm}{r^2} \Rightarrow [G][m][r^{-2}]$$

$$= (M^{-1}L^3T^{-2})(M^2)(L^{-2})$$

$$= MLT^{-2}$$

This matches the dimension of Force.

Conclusion: The formula is dimensionally correct.

5. State the effect of each of the following factors on the rate of diffusion of a fluid:

(a) Temperature;

(b) Concentration gradient;

(c) Density of the fluid.

[3 marks]

Answers to Question 5a - c

(a) Temperature: An increase in temperature increases the rate of diffusion because particles move faster.

(b) Concentration Gradient: A steeper concentration gradient increases the rate of diffusion as particles move from high to low concentration more rapidly.

(c) Density of the Fluid: Higher density slows down the rate of diffusion because particles have more resistance to movement.

6. (a) What is a projectile?

(b) What is a trajectory?

[3 marks]

Answers to Question 6a - b

6. (a) A projectile is any object that is thrown or projected into the air and continues its motion under the influence of gravity and air resistance only.

(b) A trajectory is the curved path followed by a projectile during its motion through the air.

7. (a) Explain the wave-particle duality of matter.

(b) Name one phenomenon that demonstrates that light behaves as a:

(i) wave;

(ii) particle.

[3 marks]

Answers to Question 7a - b

7. (a) The wave-particle duality of matter states that all particles, such as electrons, exhibit both wave-like and particle-like properties. This means that matter can behave like a wave in some experiments and like a particle in others.

(b) Phenomena demonstrating light’s dual behavior:

(i) Wave: Interference or diffraction patterns.

(ii) Particle: Photoelectric effect.

8. (a) State three characteristics of an elastic collision.

[3 marks]

(b) An object of mass 2 kg moving with a speed, u, collided with a stationary box. After collision, the object continued in its original direction with one-quarter of its initial speed. If the total kinetic energy of the colliding system remains constant, calculate the mass of the box.

[5 marks]

(c) A ball thrown vertically upwards to a height, h, is allowed to fall to the point of projection.
Sketch a:

(i) distance-time graph for the motion;

(ii) displacement-time graph for the motion.

[4 marks]

(d) (i) State two differences between distance and displacement.
(ii) For a given direction, state the relationship between distance and displacement.

[3 marks]

Answers to Question 8a - d

8. (a) Three characteristics of an elastic collision:

1. Total kinetic energy is conserved.

2. Total momentum is conserved.

3. No permanent deformation or heat generation occurs.

(b) Calculation of the mass of the box:

Let \( m_1 = 2 \, \text{kg} \), \( u_1 = u \), final speed of object = \( \frac{u}{4} \), and box is initially at rest.

Conservation of kinetic energy:

$$\frac{Gm}{r^2} \Rightarrow [G][m][r^{-2}]$$

$$= (M^{-1}L^3T^{-2})(M^2)(L^{-2})$$

$$= MLT^{-2}$$

Simplify and solve to find \( m_2 = \frac{15}{16} m_1 = \frac{15}{8} \) kg = 1.875 kg

(c)(i) Distance-Time Graph

(c) (ii) Displacement-Time Graph

(ii) For motion in a straight line and in one direction, displacement = distance.

(d) Differences between distance and displacement:

(i)

1. Distance is a scalar quantity; displacement is a vector quantity.

2. Distance is the total path covered; displacement is the shortest path in a straight line from start to end.

(ii) For motion in a straight line and in one direction, displacement = distance.

9. (a) State three factors that affect the rate of evaporation.

[3 marks]

(b) A heating coil of resistance, 30 Ω is connected to a 230 V supply for 3 minutes to boil a quantity of water in a container of thermal capacity 150 J K^-1. The initial temperature of the water is 50 °C and its specific heat capacity is 4.2 kJ kg^-1 K^-1. Calculate the quantity of water in the container.

[4 marks]

(c) An insulating vessel contains 80 g of a block of ice at -12 °C. If 450 g of water at 60 °C is added to the ice in the vessel:

(i) Determine whether or not the ice will melt completely;

(ii) Calculate the final temperature of the system.

Given: Specific heat capacity of ice = 2100 J kg^-1 K^-1,
Latent heat of fusion of ice = 3.33 × 10⁵ J kg^-1,
Specific heat capacity of water = 4200 J kg^-1 K^-1

[6 marks]

(d) State two differences between heat transfer by conduction and by convection.

[2 marks]

Answers to Question 9a - d

9. (a) Three factors affecting evaporation:

1. Temperature of the liquid

2. Surface area exposed

3. Air movement (wind) or humidity

(b) Energy supplied by coil:

\[ P = \frac{V^2}{R} \]

\[ P = \frac{230^2}{30} \]

\[ P = 1763.33 \, \text{W} \]

\[ Q = P \times t \]

\[ Q = 1763.33 \times 180 \]

\[ Q = 317400 \, \text{J} \]

Let mass of water be \( m \):

\[ Q = mc\Delta T + C_{\text{container}} \times \Delta T \]

[ 317400 = 4200 × m × 50

+ 150 × 50 ]

\[ 317400 = 210000m + 7500 \]

\[ 309900 = 210000m \]

\[ m = \frac{309900}{210000} \]

\[ m \approx 1.476 \, \text{kg} \]

(c)(i) Heat to warm ice to 0°C:

\[ Q_1 = mc\Delta T \]

\[ Q_1 = 0.08 \times 2100 \times 12 \]

\[ Q_1 = 2016 \, \text{J} \]

Heat to melt ice at 0°C:

\[ Q_2 = mL \]

\[ Q_2 = 0.08 \times 3.33 \times 10^5 \]

\[ Q_2 = 26640 \, \text{J} \]

Total required:

\[             Q_{\text{total}} = 2016 + 26640           \] \[             = 28656 \, \text{J}           \]

Energy from warm water:

\[ Q = mc\Delta T \]

\[ Q = 0.45 \times 4200 \times 60 \]

\[ Q = 113400 \, \text{J} \]

Conclusion: Ice will melt completely since available energy is greater than energy required.

(c)(ii) Remaining energy:

\[             Q = 113400 - 28656           \] \[             = 84744 \, \text{J}           \]

Total water mass:

\[ m = 0.45 + 0.08 = 0.53 \, \text{kg} \]

Let final temperature be \( T \):

\[ Q = mc\Delta T \]

\[ 84744 = 0.53 \times 4200 \times T \]

\[ 84744 = 2226T \]

\[ T = \frac{84744}{2226} \]

\[ T \approx 38.05^\circ C \]

(d) Differences between conduction and convection:

1. Conduction occurs in solids, convection in fluids (liquids and gases).

2. Conduction transfers heat without movement of particles; convection involves particle movement.

10. (a) Explain briefly how stationary waves are formed.

[2 marks]

(b) A standing wave formed between two points separated by a distance of 6 m is represented by the equation:

\[ y = 0.06 \cos\left(\frac{2\pi x}{3}\right) \sin(100\pi t) \] where \(x\) and \(y\) are in metres and \(t\) is in seconds.

Determine the:

(i) amplitude of the travelling waves;

(ii) speed of the travelling waves;

(iii) number of loops, \(n\), formed between the two points.

[8 marks]

(c) A transparent liquid of refractive index 1.57 is poured into a vessel to a depth of 5 cm. On top of the liquid is a layer of alcohol 10 cm deep. If the refractive index of alcohol is 1.45, determine the apparent displacement of the base of the vessel, when an observer is looking perpendicularly at the surface of the liquid.

[4 marks]

(d) Name one electromagnetic wave that is widely used in medical diagnostics.

[1 mark]

Answers to Question 10 (a) - (d)

10. (a) Stationary waves are formed when two waves of the same frequency and amplitude travel in opposite directions and interfere. This results in points of no displacement (nodes) and points of maximum displacement (antinodes).

(b) Given:

\[ y = 0.06 \cos\left(\frac{2\pi x}{3}\right) \sin(100\pi t) \]

(i) Amplitude of the travelling waves = 0.06 m

(ii) Comparing with standard form:

\[ y = A \cos(kx) \sin(\omega t) \] where \(k = \frac{2\pi}{\lambda}\) and \(\omega = 2\pi f\)

\[ k = \frac{2\pi}{3} \Rightarrow \lambda = 3 \, \text{m} \]

    \[     \omega = 100\pi     \]

    \[     f = \frac{100\pi}{2\pi} = 50 \, \text{Hz}     \]

\[ v = f \lambda = 50 \times 3 = 150 \, \text{m/s} \]

Speed of the travelling waves = 150 m/s

(iii) Distance between nodes = \(\frac{\lambda}{2} = \frac{3}{2} = 1.5 \, \text{m}\)

\[ \frac{6}{1.5} = 4 \, \text{loops} \]

Number of loops, \(n = 4\)

(c) Apparent depth = \(\frac{\text{real depth}}{\text{refractive index}}\)

Apparent depth of alcohol layer:

\[ d_1 = \frac{10}{1.45} = 6.90 \, \text{cm} \]

Apparent depth of liquid layer:

\[ d_2 = \frac{5}{1.57} = 3.18 \, \text{cm} \]

Total apparent depth = \(6.90 + 3.18 = 10.08 \, \text{cm}\)

Real depth = \(10 + 5 = 15 \, \text{cm}\)

\[ \text{Apparent displacement}\] \[= 15 - 10.08\] \[= 4.92 \, \text{cm} \]

Apparent displacement = 4.92 cm

(d) X-rays

11. (a) (i) What is an electrical circuit?

(ii) List four basic components of any electrical circuit giving an example of each.

[6 marks]

(b)

(i) Define the term relative permittivity.

(ii) A parallel plate capacitor of area \(5.0 \times 10^{-2} \, \text{m}^2\) has a plate separation of 2 mm in air. If a material of thickness 1.5 mm and relative permittivity 4.0 fills the gap between the plates, calculate the capacitance of the capacitor.

\[\varepsilon_0 = 8.9 \times 10^{-12} \, \text{F m}^{-1}\]

[6 marks]

(c) In a metre bridge experiment, a student was unable to find the balance point. Give two reasons for the occurrence.

[2 marks]

(d) State one use of the metre bridge circuit.

[1 mark]

Answers to Question 11 (a) - (d)

11. (a) (i) An electrical circuit is a closed path through which electric current flows, consisting of electrical components connected by conductors.

(ii) Four basic components of any electrical circuit and their examples:

• Resistor: Limits the flow of current (e.g., carbon resistor)
• Capacitor: Stores electrical energy (e.g., ceramic capacitor)
• Inductor: Opposes change in current (e.g., coil of wire)
• Power source: Provides energy to the circuit (e.g., battery)

(b) (i) Relative permittivity is the ratio of the permittivity of a material to the permittivity of free space. It indicates how much the material can increase the capacitance compared to air.

(ii) Given:

• Area, \( A = 5.0 \times 10^{-2} \, \text{m}^2 \)
• Plate separation, \( d = 2 \, \text{mm} = 2 \times 10^{-3} \, \text{m} \)
• Material thickness, \( t = 1.5 \, \text{mm} = 1.5 \times 10^{-3} \, \text{m} \)
• Air gap thickness = \( d - t = 0.5 \times 10^{-3} \, \text{m} \)
• Relative permittivity, \( \varepsilon_r = 4.0 \)
• Vacuum permittivity, \( \varepsilon_0 = 8.9 \times 10^{-12} \, \text{F/m} \)

Capacitance of a capacitor with two dielectrics in series:

\[ \frac{1}{C} = \frac{d_1}{\varepsilon_0 A} + \frac{d_2}{\varepsilon_r \varepsilon_0 A} \] where:
\( d_1 = 0.5 \times 10^{-3} \, \text{m} \) (air)
\( d_2 = 1.5 \times 10^{-3} \, \text{m} \) (material)

Substituting values:

\[ \frac{1}{C} =\] \[\frac{0.5 \times 10^{-3}}{8.9 \times 10^{-12} \times 5.0 \times 10^{-2}} +\] \[\frac{1.5 \times 10^{-3}}{4 \times 8.9 \times 10^{-12} \times 5.0 \times 10^{-2}} \]

\[ \frac{1}{C} = \frac{0.5 \times 10^{-3}}{4.45 \times 10^{-13}} +\] \[\frac{1.5 \times 10^{-3}}{1.78 \times 10^{-12}} \Rightarrow \frac{1}{C} =\]\[ 1.1236 \times 10^{9} + 8.4269 \times 10^{8}\] \[= 1.9663 \times 10^{9} \]

\[ C = \frac{1}{1.9663 \times 10^9}\] \[= 5.086 \times 10^{-10} \, \text{F}\] \[= \boxed{508.6 \, \text{pF}} \]

(c) Two reasons why a student may be unable to find the balance point in a metre bridge experiment:

• Poor electrical contact at the junctions
• The resistance of the unknown or known resistor is too high or too low, moving the balance point outside the bridge wire

(d) One use of the metre bridge circuit is to determine an unknown resistance using the principle of a Wheatstone bridge.

12. (a) Distinguish between \(\beta\) and \(\gamma\) radiations under the following headings:

(i) Nature;

(ii) Charge;

(iii) Speed;

[3 marks]

(b) State two:

(i) Similarities;

(ii) Differences;

between photoelectrons and thermoelectrons.

[4 marks]

(c) A metal, X has a work function of 2.0 eV.

(i) Explain the underlined statement.

(ii) If X is illuminated with light of wavelength \(4.5 \times 10^{-7} \, \text{m}\), calculate the:

(A) Cut-off wavelength;

(β) Maximum energy of the liberated electrons;

(γ) Stopping potential.

[\(h = 6.6 \times 10^{-34} \, \text{Js}\), \(c = 3.0 \times 10^8 \, \text{ms}^{-1}\), \(1 \, \text{eV} = 1.6 \times 10^{-19} \, \text{J}\), \(e = 1.6 \times 10^{-19} \, \text{C}\)]

[8 marks]

Answers to Question 12 (a) – (c)

12. (a) Differences between \(\beta\) and \(\gamma\) radiations:

• (i) Nature: \(\beta\)-radiation consists of fast-moving electrons or positrons, while \(\gamma\)-radiation is electromagnetic radiation (photons).
• (ii) Charge: \(\beta\)-particles carry a negative (or positive, for positrons) charge; \(\gamma\)-rays are neutral (no charge).
• (iii) Speed: \(\beta\)-particles travel at speeds less than the speed of light; \(\gamma\)-rays travel at the speed of light.

(b) Similarities and differences between photoelectrons and thermoelectrons:

(i) Similarities:

• Both are electrons emitted from the surface of a metal.
• Both involve overcoming the work function of the metal.

(ii) Differences:

• Photoelectrons are emitted due to the absorption of photons (light energy).
• Thermoelectrons are emitted due to the heating of the metal (thermal energy).

(c) Given:

Work function, \[\phi = 2.0 \, \text{eV}\] \[= 2.0 \times 1.6 \times 10^{-19}\] \[= 3.2 \times 10^{-19} \, \text{J}\]

Wavelength, \(\lambda = 4.5 \times 10^{-7} \, \text{m}\)

\[h = 6.6 \times 10^{-34} \, \text{Js}, \quad\] \[c = 3.0 \times 10^8 \, \text{m/s}, \quad\] \[e = 1.6 \times 10^{-19} \, \text{C}\]

(i) The work function of 2.0 eV means the minimum energy required to eject an electron from the surface of metal X is 2.0 electron volts.

(ii) Calculations:

(A) Cut-off wavelength, \(\lambda_0\):

\[ \phi = \frac{hc}{\lambda_0} \Rightarrow \lambda_0 = \frac{hc}{\phi} \]

\[ \lambda_0 = \frac{6.6 \times 10^{-34} \times 3.0 \times 10^8}{3.2 \times 10^{-19}}\] \[= 6.19 \times 10^{-7} \, \text{m} \]

(β) Maximum energy of liberated electrons, \(E_k\):

\[ E = \frac{hc}{\lambda}\] \[= \frac{6.6 \times 10^{-34} \times 3.0 \times 10^8}{4.5 \times 10^{-7}}\] \[= 4.4 \times 10^{-19} \, \text{J} \]

\[ E_k = E - \phi\] \[= 4.4 \times 10^{-19} - 3.2 \times 10^{-19}\] \[= 1.2 \times 10^{-19} \, \text{J} \]

(γ) Stopping potential, \(V_s\):

\[ V_s = \frac{E_k}{e}\] \[= \frac{1.2 \times 10^{-19}}{1.6 \times 10^{-19}}\] \[= 0.75 \, \text{V} \]